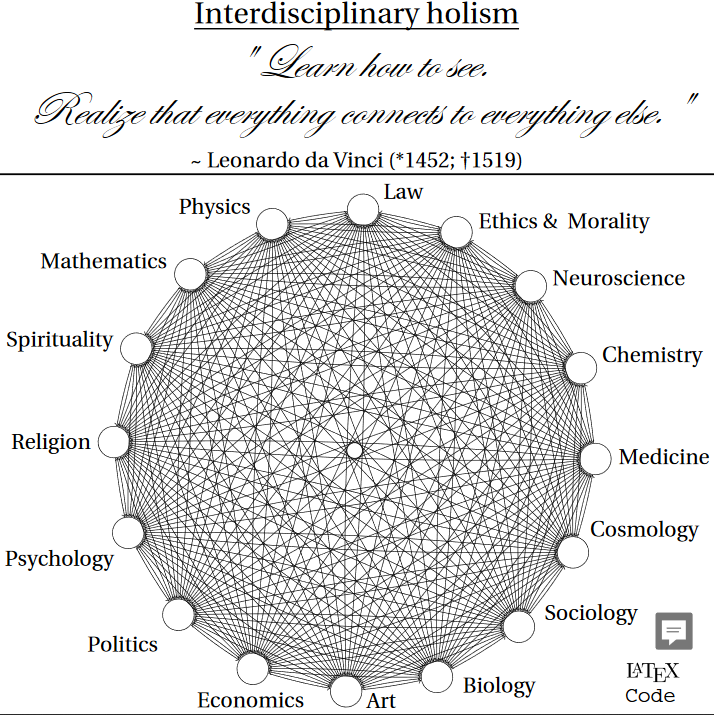
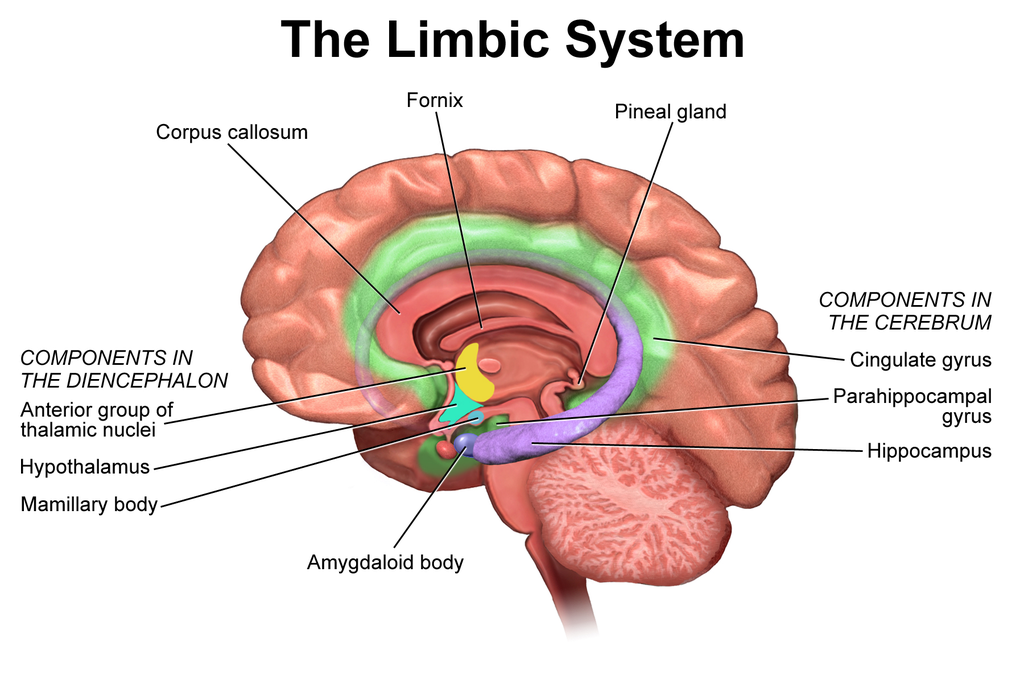
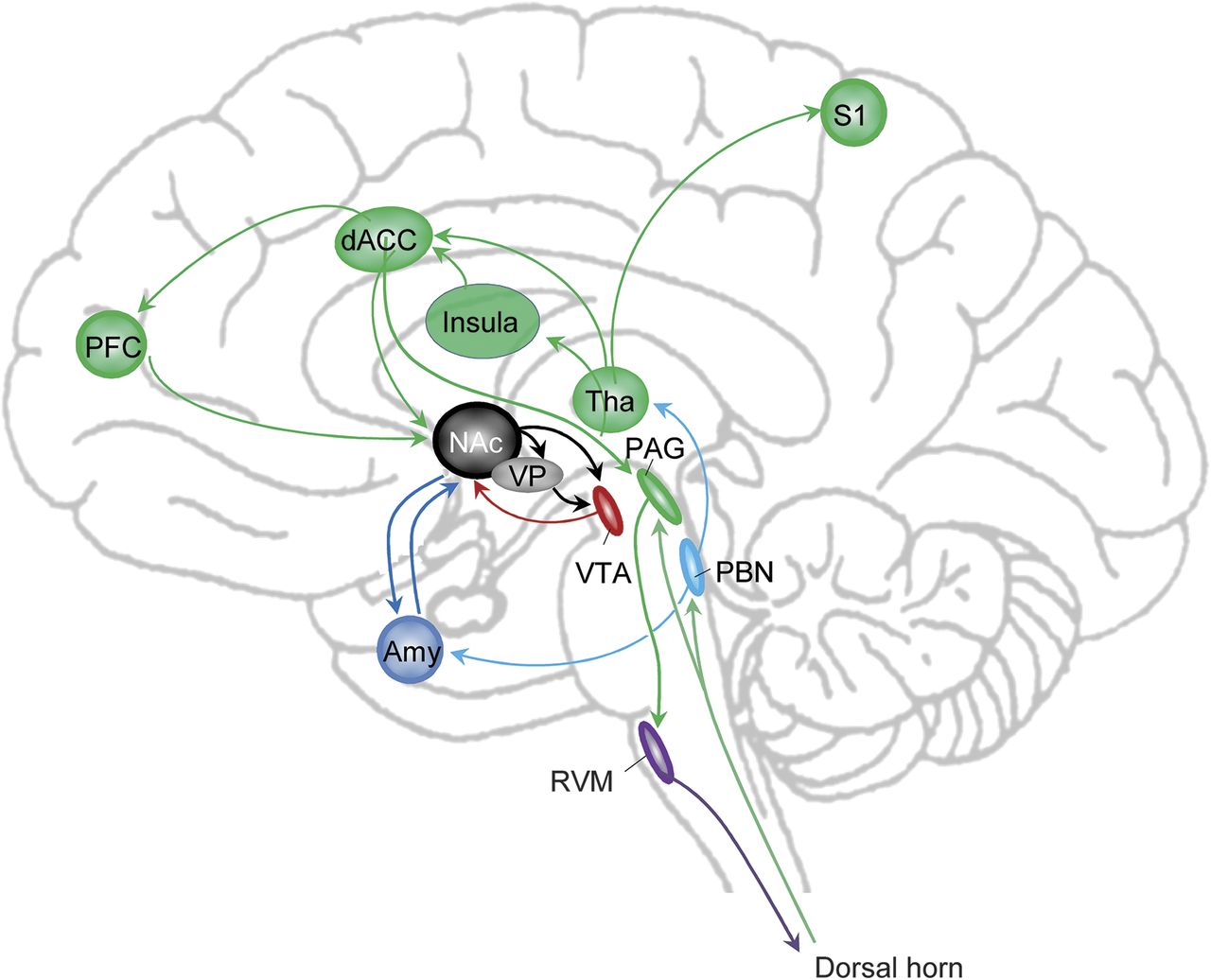
Interdisciplinary matrices
The interactions between disciplines can be geometrically conceptualised as a cross-polytope, viz., each discipline is a node in the polytope.
An n-dimensional cross-polytope (synonymously referred to as “orthoplex”) can be defined as the closed unit ball in the ℓ1-norm on Rn:
${\displaystyle \{x\in \mathbb {R} ^{n}:\|x\|_{1}\leq 1\}.}$
but see en.wikipedia.org/wiki/Cross-polytope
Generically speaking, each set of k+1 orthogonal vertices corresponds to a distinct k-dimensional component which contains them. The number of k-dimensional components (vertices, edges, faces, …, facets) in an n-dimensional cross-polytope is given by the following equation:
${\displaystyle 2^{k+1}{n \choose {k+1}}}$
Typesetting in
${\LaTeX\kern .15em2_{\textstyle \varepsilon }}$
and MathJaxTM
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary[topaths]
% A counter, since TikZ is not clever enough (yet) to handle
% arbitrary angle systems.
\newcount\mycount
\begin{document}
\begin{tikzpicture}[transform shape]
%the multiplication with floats is not possible. Thus I split the loop in two.
\foreach \number in {1,...,8}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 0
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {9,...,16}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 22.5
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {1,...,15}{
\mycount=\number
\advance\mycount by 1
\foreach \numbera in {\the\mycount,...,16}{
\path (N-\number) edge[->,bend right=3] (N-\numbera) edge[<-,bend
left=3] (N-\numbera);
}
}
\end{tikzpicture}
\end{document}
% A complete graph
% Author: Quintin Jean-Noël
% http://moais.imag.fr/membres/jean-noel.quintin/
#library(devtools)
#install_github("schloerke/geozoo")
#install.packages("geozoo")
cross.polytope(p = 16)
Arguments
p= dimension of object
Value
- points
- location of points
- edges
- edges of the object
see also schloerke.com/geozoo/cube/
References
Plain numerical DOI: 10.1021/acs.joc.6b02599
DOI URL
directSciHub download
Show/hide publication abstract
Knuth, Donald E. (2013), “Two thousand years of combinatorics”, in Wilson, Robin; Watkins, John J., Combinatorics: Ancient and Modern, Oxford University Press, pp. 7–37, ISBN 0191630624.
Plain numerical DOI: 10.1002/bdrc.20196
DOI URL
directSciHub download
Show/hide publication abstract
Show/hide publication abstract
Plain numerical DOI: 10.1111/j.1462-2920.2009.01995.x
DOI URL
directSciHub download
Show/hide publication abstract
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
(CC) 2016—2019 | #Sitemap | #Sitemap | §Dataprotection according to GDPR |
This project was funded by the EU Marie Curie Initial Training Network FP7-PEOPLE-2013-ITN-604764
→ Primary goals of research and innovation policy as defined by the European Comission: Open Innovation, Open Science, Open to the World.
Legal disclaimer: The interdisciplinary Marie Curie CogNovo program has been intentionally designed by the European Union and the University of Plymouth (United Kingdom) to discuss and disseminate a wide view on a diverse spectrum of topics including psychology, neuroscience, current affairs, basic science, humanities, and the arts, inter alia. Note that the views and opinions expressed on this website do not necessarily represent the opinions of any of the institutions mentioned on this website and belong exclusively to author. The CogNovo program explicitly emphasises cognitive and social innovation, the generation of new ideas and perspectives, and the probing of boundaries, but see https://www.cognovo.eu/about/
![page-divider-0[1]](https://cognitive-liberty.online/wp-content/uploads/page-divider-01-e1545895146246.png "Möbius animation")
Leave a Reply