http://holism.ga
Complete knowledge Graph (Cross-disciplinary Polytope Δ16)Interdisciplinary matricesCommentLaTeX CodeR codeQR codeReferencesContactMisc
Show as Latex PDF
Page / 2
Zoom 100%
[{{type}} Annotation]
Page / 2
Zoom 100%

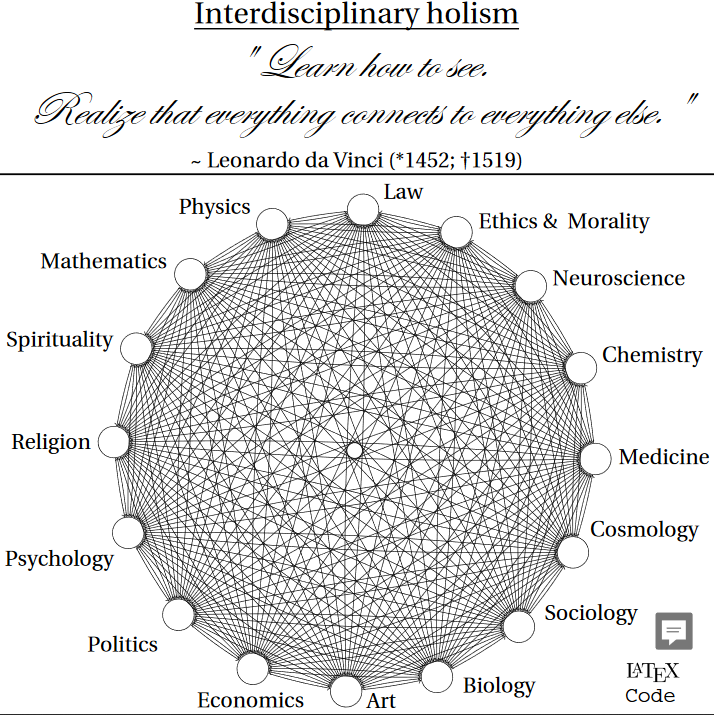
Interdisciplinary matrices

The interactions between disciplines can be geometrically conceptualised as a cross-polytope, viz., each discipline is a node in the polytope.

An n-dimensional cross-polytope (synonymously referred to as “orthoplex”) can be defined as the closed unit ball in the ℓ1-norm on Rn:
{x∈Rn:‖x‖1≤1}.

but see en.wikipedia.org/wiki/Cross-polytope

Generically speaking, each set of k+1 orthogonal vertices corresponds to a distinct k-dimensional component which contains them. The number of k-dimensional components (vertices, edges, faces, …, facets) in an n-dimensional cross-polytope is given by the following equation:

2k+1(nk+1)

Typesetting in
LATEX2ε

and MathJaxTM

Leave a Reply

Your email address will not be published. Required fields are marked *

2 + 7 =

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary[topaths]
% A counter, since TikZ is not clever enough (yet) to handle
% arbitrary angle systems.
\newcount\mycount
\begin{document}
\begin{tikzpicture}[transform shape]
%the multiplication with floats is not possible. Thus I split the loop in two.
\foreach \number in {1,...,8}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 0
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {9,...,16}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 22.5
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {1,...,15}{
\mycount=\number
\advance\mycount by 1
\foreach \numbera in {\the\mycount,...,16}{
\path (N-\number) edge[->,bend right=3] (N-\numbera) edge[<-,bend
left=3] (N-\numbera);
}
}
\end{tikzpicture}
\end{document}
% A complete graph
% Author: Quintin Jean-Noël
% http://moais.imag.fr/membres/jean-noel.quintin/
\documentclass{article} \usepackage{tikz} \usetikzlibrary[topaths] % A counter, since TikZ is not clever enough (yet) to handle % arbitrary angle systems. \newcount\mycount Unknown environment 'document' % A complete graph % Author: Quintin Jean-Noël % http://moais.imag.fr/membres/jean-noel.quintin/
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary[topaths]
% A counter, since TikZ is not clever enough (yet) to handle
% arbitrary angle systems.
\newcount\mycount
\begin{document}
\begin{tikzpicture}[transform shape]
%the multiplication with floats is not possible. Thus I split the loop in two.
\foreach \number in {1,...,8}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 0
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {9,...,16}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 22.5
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {1,...,15}{
\mycount=\number
\advance\mycount by 1
\foreach \numbera in {\the\mycount,...,16}{
\path (N-\number) edge[->,bend right=3] (N-\numbera)  edge[<-,bend
left=3] (N-\numbera);
}
}
\end{tikzpicture}
\end{document}
% A complete graph
% Author: Quintin Jean-Noël
% http://moais.imag.fr/membres/jean-noel.quintin/
#library(devtools)
#install_github("schloerke/geozoo")
#install.packages("geozoo")
cross.polytope(p = 16)
#library(devtools) #install_github("schloerke/geozoo") #install.packages("geozoo") cross.polytope(p = 16)
#library(devtools)
#install_github("schloerke/geozoo")
#install.packages("geozoo")
cross.polytope(p = 16)
Arguments
p = dimension of object
Value
points
location of points
edges
edges of the object

see also schloerke.com/geozoo/cube/

http://holism.ga

References

Ash, M. G.. (1998). Gestalt psychology in German culture, 1890-1967 : holism and the quest for objectivity. Cambridge Studies in the History of Psychology

Plain numerical DOI: 10.1021/acs.joc.6b02599
DOI URL
directSciHub download

Knuth, Donald E. (2013), “Two thousand years of combinatorics”, in Wilson, Robin; Watkins, John J., Combinatorics: Ancient and Modern, Oxford University Press, pp. 7–37, ISBN 0191630624.

Rosenberg, E., & Zilber-Rosenberg, I.. (2011). Symbiosis and development: The hologenome concept. Birth Defects Research Part C – Embryo Today: Reviews

Plain numerical DOI: 10.1002/bdrc.20196
DOI URL
directSciHub download

Rosenberg, E., & Zilber-Rosenberg, I.. (2008). Role of microorganisms in the evolution of animals and plants:The hologenome theory of evolution. F. E. M. S. Microbiol. Rev., 32, 723–735.
Rosenberg, E., Sharon, G., & Zilber-Rosenberg, I.. (2009). The hologenome theory of evolution contains Lamarckian aspects within a Darwinian framework. Environmental Microbiology, 11(12), 2959–2962.

Plain numerical DOI: 10.1111/j.1462-2920.2009.01995.x
DOI URL
directSciHub download

    Please prove you are human by selecting the Key.

    Visual Portfolio, Posts & Image Gallery for WordPress
    Show All
    AI
    Anthropology
    Art
    Articles
    Books
    Cognitive science
    Covid
    Cybernetics
    Documentary
    Economics
    Education
    Embodied Cognition
    General
    General psychology
    History
    Legal
    Logic & Reasoning
    Monetary system
    Neuropolitics
    Neuroscience
    Philosophy
    Politics
    Primary documents
    Psychiatry
    Psychopolitics
    Science
    Social psychology
    Sociology
    Software
    Video
    Load more Loading more... You’ve reached the end of the list

    • Intelligent search function

      More results...

      Generic selectors
      Exact matches only
      Search in title
      Search in content
      Post Type Selectors
      Search in posts
      Search in pages
    Further Links: https://psilocybin-research.com http://entheogen-science.de

    Contextually related entries:

    de Germannl Dutchfr Frenches Spanishen Englishaf Afrikaanssq Albanianam Amharicar Arabichy Armenianaz Azerbaijanieu Basquebe Belarusianbn Bengalibs Bosnianbg Bulgarianca Catalanceb Cebuanony Chichewazh-CN Chinese (Simplified)zh-TW Chinese (Traditional)co Corsicanhr Croatiancs Czechda Danisheo Esperantoet Estoniantl Filipinofi Finnishfy Frisiangl Galicianka Georgianel Greekgu Gujaratiht Haitian Creoleha Hausahaw Hawaiianiw Hebrewhi Hindihmn Hmonghu Hungarianis Icelandicig Igboid Indonesianga Irishit Italianja Japanesejw Javanesekn Kannadakk Kazakhkm Khmerko Koreanku Kurdish (Kurmanji)ky Kyrgyzlo Laola Latinlv Latvianlt Lithuanianlb Luxembourgishmk Macedonianmg Malagasyms Malayml Malayalammt Maltesemi Maorimr Marathimn Mongolianmy Myanmar (Burmese)ne Nepalino Norwegianps Pashtofa Persianpl Polishpt Portuguesepa Punjabiro Romanianru Russiansm Samoangd Scottish Gaelicsr Serbianst Sesothosn Shonasd Sindhisi Sinhalask Slovaksl Slovenianso Somalisu Sundanesesw Swahilisv Swedishtg Tajikta Tamilte Teluguth Thaitr Turkishuk Ukrainianur Urduuz Uzbekvi Vietnamesecy Welshxh Xhosayi Yiddishyo Yorubazu Zulu
    en English