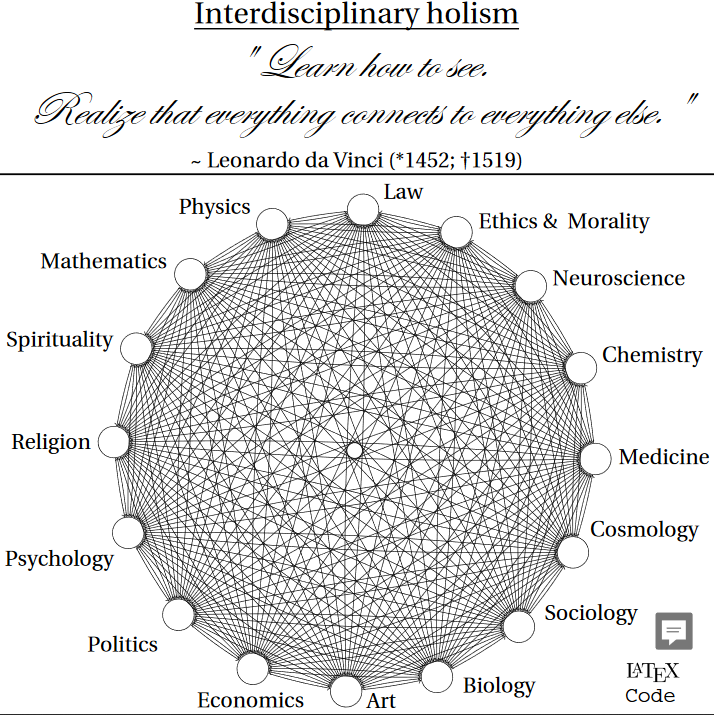
Interdisciplinary matrices
The interactions between disciplines can be geometrically conceptualised as a cross-polytope, viz., each discipline is a node in the polytope.
An n-dimensional cross-polytope (synonymously referred to as “orthoplex”) can be defined as the closed unit ball in the ℓ1-norm on Rn:
${\displaystyle \{x\in \mathbb {R} ^{n}:\|x\|_{1}\leq 1\}.}$
but see en.wikipedia.org/wiki/Cross-polytope
Generically speaking, each set of k+1 orthogonal vertices corresponds to a distinct k-dimensional component which contains them. The number of k-dimensional components (vertices, edges, faces, …, facets) in an n-dimensional cross-polytope is given by the following equation:
${\displaystyle 2^{k+1}{n \choose {k+1}}}$
Typesetting in
${\LaTeX\kern .15em2_{\textstyle \varepsilon }}$
and MathJaxTM
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary[topaths]
% A counter, since TikZ is not clever enough (yet) to handle
% arbitrary angle systems.
\newcount\mycount
\begin{document}
\begin{tikzpicture}[transform shape]
%the multiplication with floats is not possible. Thus I split the loop in two.
\foreach \number in {1,...,8}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 0
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {9,...,16}{
% Computer angle:
\mycount=\number
\advance\mycount by -1
\multiply\mycount by 45
\advance\mycount by 22.5
\node[draw,circle,inner sep=0.25cm] (N-\number) at (\the\mycount:5.4cm) {};
}
\foreach \number in {1,...,15}{
\mycount=\number
\advance\mycount by 1
\foreach \numbera in {\the\mycount,...,16}{
\path (N-\number) edge[->,bend right=3] (N-\numbera) edge[<-,bend
left=3] (N-\numbera);
}
}
\end{tikzpicture}
\end{document}
% A complete graph
% Author: Quintin Jean-Noël
% http://moais.imag.fr/membres/jean-noel.quintin/
#library(devtools)
#install_github("schloerke/geozoo")
#install.packages("geozoo")
cross.polytope(p = 16)
Arguments
p= dimension of object
Value
- points
- location of points
- edges
- edges of the object
see also schloerke.com/geozoo/cube/
References
Plain numerical DOI: 10.1021/acs.joc.6b02599
DOI URL
directSciHub download
Show/hide publication abstract
Knuth, Donald E. (2013), “Two thousand years of combinatorics”, in Wilson, Robin; Watkins, John J., Combinatorics: Ancient and Modern, Oxford University Press, pp. 7–37, ISBN 0191630624.
Plain numerical DOI: 10.1002/bdrc.20196
DOI URL
directSciHub download
Show/hide publication abstract
Show/hide publication abstract
Plain numerical DOI: 10.1111/j.1462-2920.2009.01995.x
DOI URL
directSciHub download





























































 This project was funded by the
This project was funded by the 


![Möbius animation page-divider-0[1]](https://cognitive-liberty.online/wp-content/uploads/page-divider-01-e1545895146246.png)
Leave a Reply